boltdb 是市面上为数不多的纯 go 语言开发的、单机 KV 库。boltdb 基于 Howard Chu’s LMDB 项目 ,实现的比较清爽,去掉单元测试和适配代码,核心代码大概四千多行。简单的 API、简约的实现,也是作者的意图所在。由于作者精力所限,原 boltdb 已经封版,不再更新。若想改进,提交新的 pr,建议去 etcd 维护的 fork 版本 bbolt。
为了方便,本系列导读文章仍以不再变动的原 repo 为基础。该项目麻雀虽小,五脏俱全,仅仅四千多行代码,就实现了一个基于 B+ 树索引、支持一写多读事务的单机 KV 引擎。代码本身简约朴实、注释得当,如果你是 go 语言爱好者、如果对 KV 库感兴趣,那 boltdb 绝对是不可错过的一个 repo。
本系列计划分成三篇文章,依次围绕数据组织、索引设计、事务实现等三个主要方面对 boltdb 源码进行剖析。由于三个方面不是完全正交解耦的,因此叙述时会不可避免的产生交织,读不懂时,暂时略过即可,待有全貌,再回来梳理。本文是第一篇, boltdb 数据组织。
概览
数据库中常用的索引设计有两种,一个是 B+ 树,一个是 LSM-tree。B+ 树比较经典,比如说传统单机数据库 mysql 就是 B+ 树索引,它对快速读取和范围查询(range query)比较友好。 LSM-tree 是近年来比较流行的索引结构,Bigtable、LevelDB、RocksDB 都有它的影子;前面文章也有提到,LSM-tree 使用 WAL 和多级数据组织以牺牲部分读性能,换来强悍的随机写性能。因此,这也是一个经典的取舍问题。
BoltDB 在逻辑上以桶来组织数据,一个桶可以看做一个命名空间,是一组 KV 对的集合,和对象存储的桶概念类似。每个桶对应一棵 B+ 树,命名空间是可以嵌套的,因此 BoltDB 的 Bucket 间也是允许嵌套的。在实现上来说,子 bucket 的 root node 的 page id 保存在父 bucket 叶子节点上实现嵌套。
每个 db 文件,是一组树形组织的 B+ 树。我们知道对于 B+ 树来说,分支节点用于查找,叶子节点存数据。
- 顶层 B+ 树,比较特殊,称为 root bucket,其所有叶子节点保存的都是子 bucket B+ 树根的 page id 。
- 其他 B+ 树,不妨称之为 data bucket,其叶子节点可能是正常用户数据,也可能是子 bucket B+ 树根的 page id。
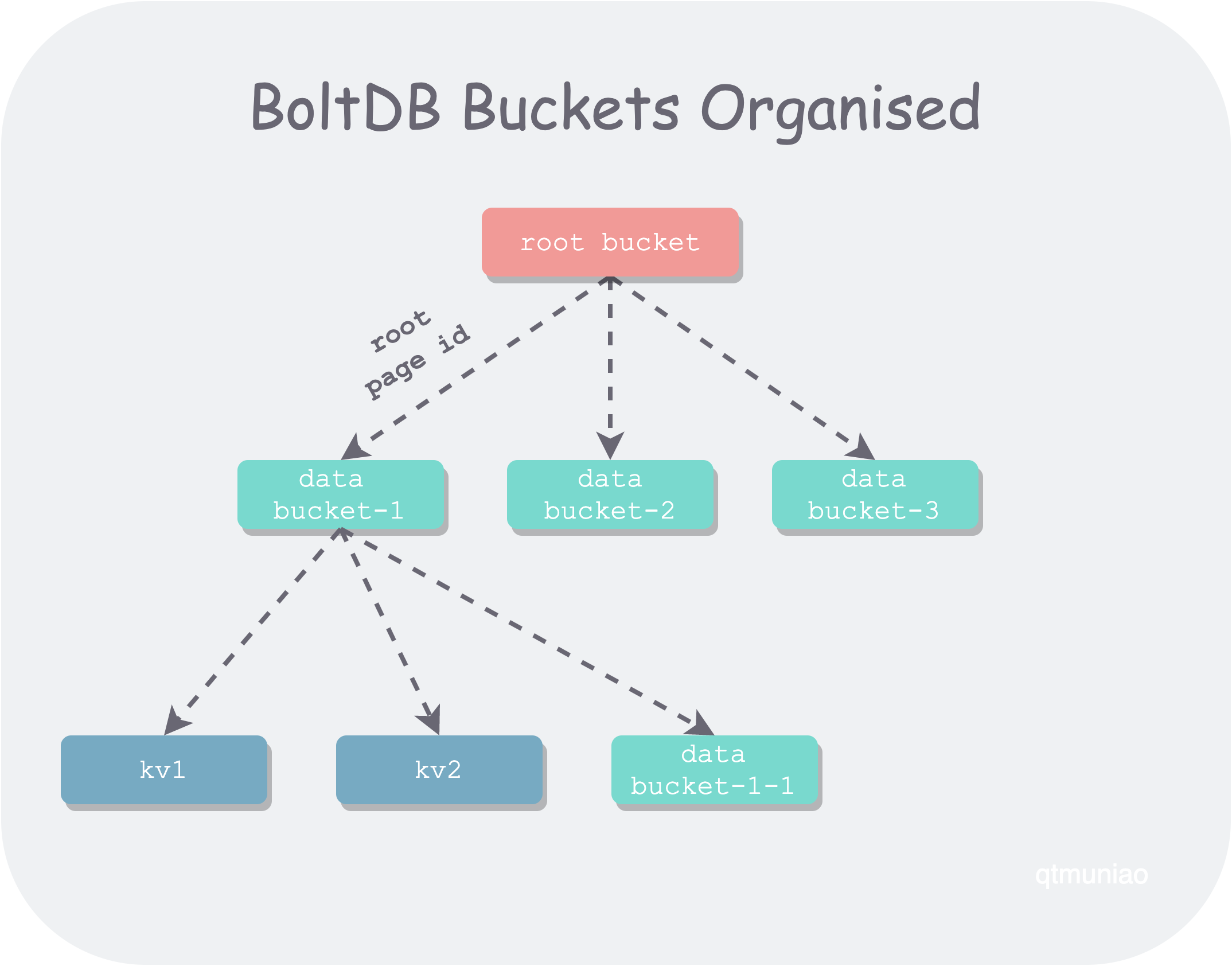
相比普通 B+ 树,boltdb 的 B+ 树有几点特殊之处:
- 节点的分支个数不是一个固定范围,而是依据其所存元素大小之和来限制的,这个上限即为页大小。
- 其分支节点(branch node)所存分支的 key,是其所指向分支的最小 key。
- 所有叶子节点并没有通过链表首尾相接起来。
- 没有保证所有的叶子节点都在同一层。
在代码组织上,boltdb 索引相关的源文件如下:
- bucket.go:对 bucket 操作的高层封装。包括kv 的增删改查、子bucket 的增删改查以及 B+ 树拆分和合并。
- node.go:对 node 所存元素和 node 间关系的相关操作。节点内所存元素的增删、加载和落盘,访问孩子兄弟元素、拆分与合并的详细逻辑。
- cursor.go:实现了类似迭代器的功能,可以在 B+ 树上的叶子节点上进行随意游走。
本文主要分三部分,由局部到整体来一步步揭示 BoltDB 是如何进行索引设计的。首先会拆解树的基本单元,其次剖析 bucket 的遍历实现,最后分析树的生长和平衡过程。
作者:木鸟杂记 https://www.qtmuniao.com/2020/12/14/bolt-index-design, 转载请注明出处
基本单元——节点(Node)
B+ 树的基本构成单元是节点(node),对应在上一篇中提到过文件系统中存储的页(page),节点包括两种类型,分支节点(branch node)和叶子节点(leaf node)。但在实现时,他们复用了同一个结构体,并通过一个标志位 isLeaf 来区分:
1 | // node 表示内存中一个反序列化后的 page |
node/page 转换
page 和 node 的对应关系为:文件系统中一组连续的物理 page,加载到内存成为一个逻辑 page ,进而转化为一个 node。下图为一个在文件系统上占用两个 pagesize 空间的一段连续数据 ,首先 mmap 到内存空间,转换为 page 类型,然后通过 node.read 转换为 node 的过程。
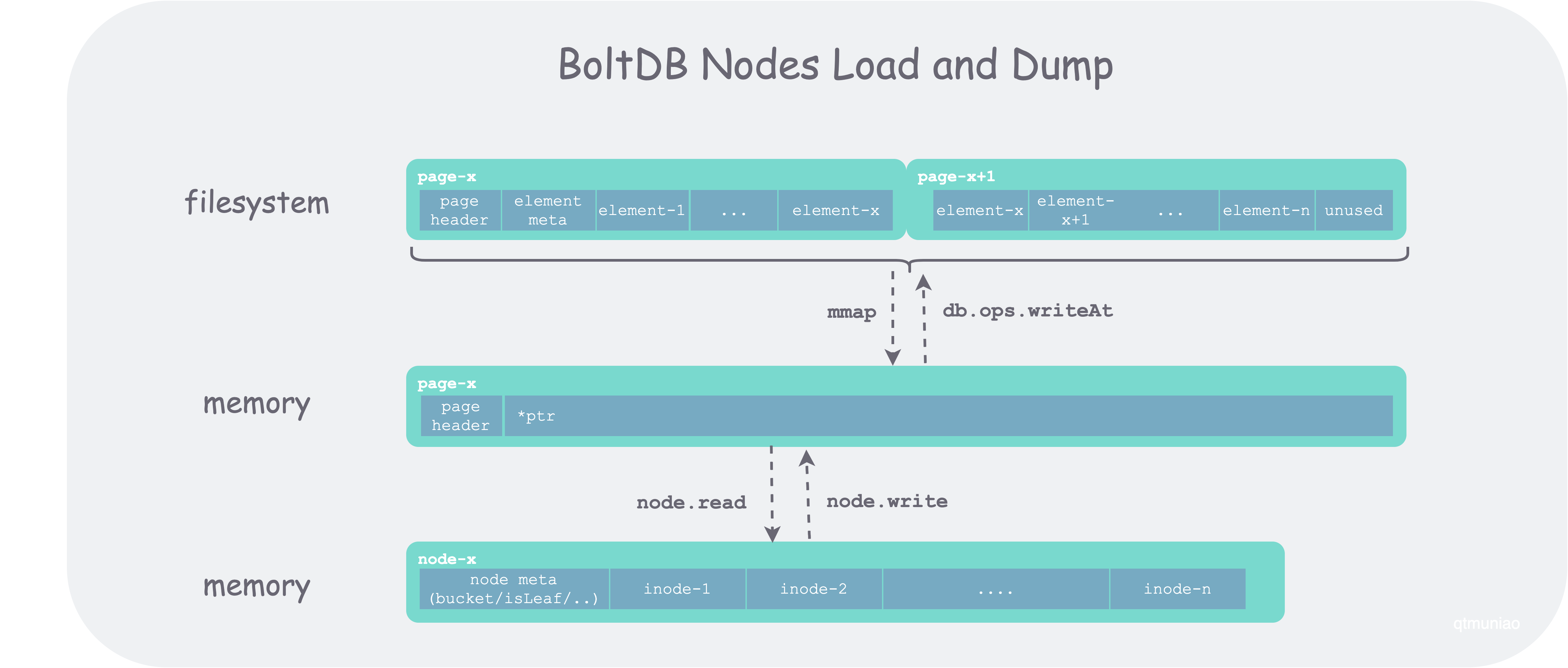
其中 node.read 将 page 转换为 node 的代码如下:
1 | // read 函数通过 mmap 读取 page,并转换为 node |
node 元素 inode
inode 表示 node 所含的内部元素,分支节点和叶子节点也复用同一个结构体。对于分支节点,单个元素为 key+引用;对于叶子节点,单个元素为用户 kv 数据。
注意到这里对其他节点的引用类型为 pgid ,而非 node*。这是因为 inode 中指向的元素并不一定加载到了内存。 boltdb 在访问 B+ 树时,会按需将访问到的 page 转化为 node,并将其指针存在父节点的 children 字段中, 具体的加载顺序和逻辑在后面小结会详述。
1 | type inode struct { |
inode 会在 B+ 树中进行路由——二分查找时使用。
新增元素
所有的数据新增都发生在叶子节点,如果新增数据后 B+ 树不平衡,之后会通过 node.spill 来进行拆分调整。主要代码如下:
1 | // put inserts a key/value. |
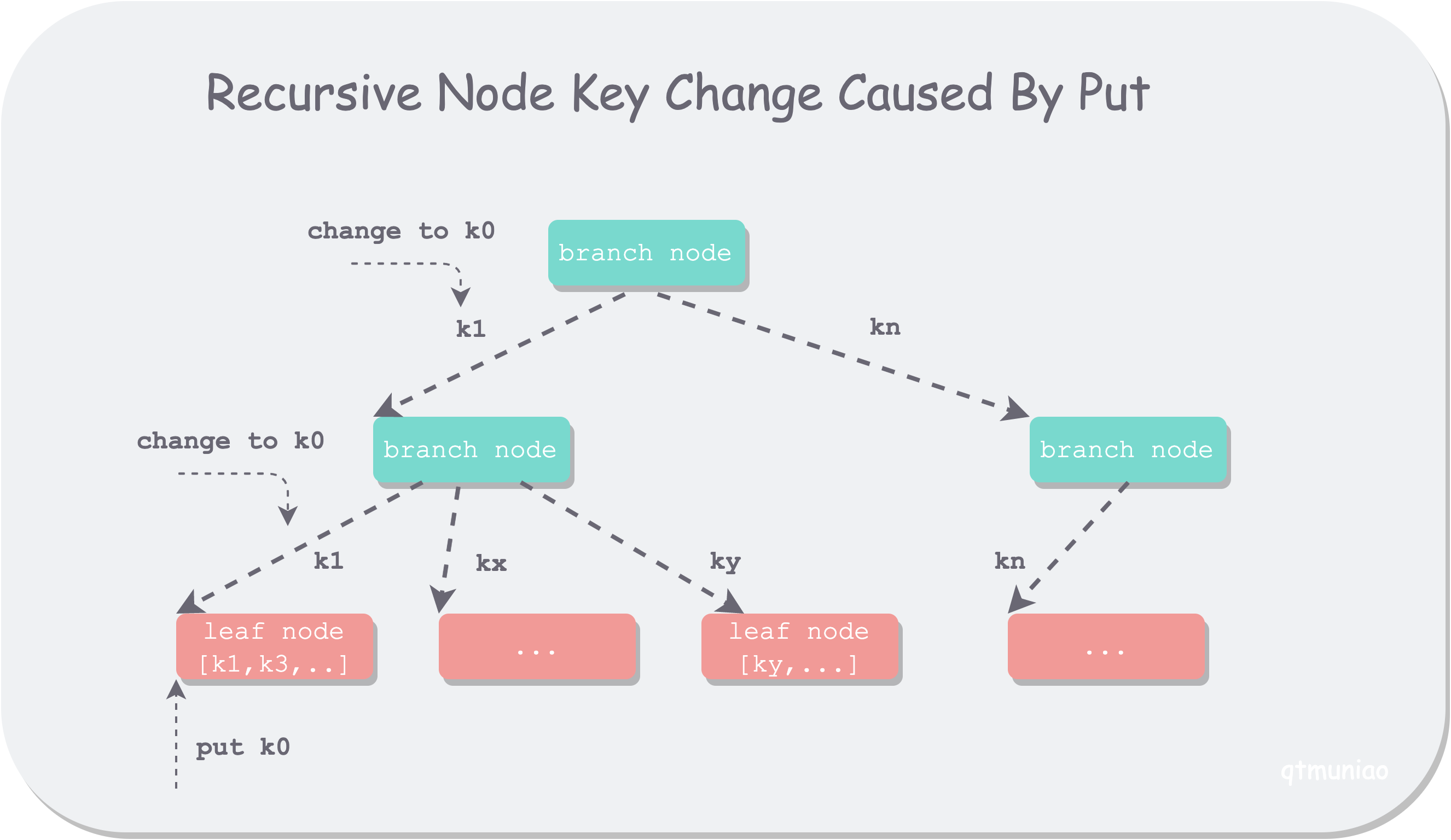
该函数的主干逻辑比较简单,就是二分查找到待插入位置,如果是覆盖写则直接覆盖;否则就要新增一个元素,并整体右移,腾出插入位置。 但是该函数签名很有意思,同时有 oldKey 和 newKey ,开始时感觉很奇怪。其调用代码有两处:
- 在叶子节点插入用户数据时,
oldKey等于newKey,此时这两个参数是有冗余的。 - 在
spill阶段调整 B+ 树时,oldKey可能不等于newKey,此时是有用的,但从代码上来看,用处仍然很隐晦。
在和朋友讨论后,大致得出如下结论:为了避免在叶子节点最左侧插入一个很小的值时,引起祖先节点的 node.key 的链式更新,而将更新延迟到了最后 B+ 树调整阶段(spill 函数)进行统一处理 。此时,需要利用 node.put 函数将最左边的 node.key 更新为 node.inodes[0].key:
1 | // 该代码片段在 node.spill 函数中 |
节点遍历
由于 Golang 不支持 Python 中类似 yield 机制,boltdb 使用栈保存遍历上下文实现了一个树节点顺序遍历的迭代器:cursor。在逻辑上可以理解为对某 B+ 树叶子节点所存元素遍历的迭代器。之前提到,boltdb 的 B+ 树没有使用链表将所有叶子节点串起来,因此需要一些额外逻辑来进行遍历中各种细节的处理。
这么实现增加了遍历的复杂度,但是减少了维持 B+ 树平衡性质的难度,也是一种取舍。当然,最重要的是为了通过 COW 实现事务时,避免链式更新所有前驱节点。
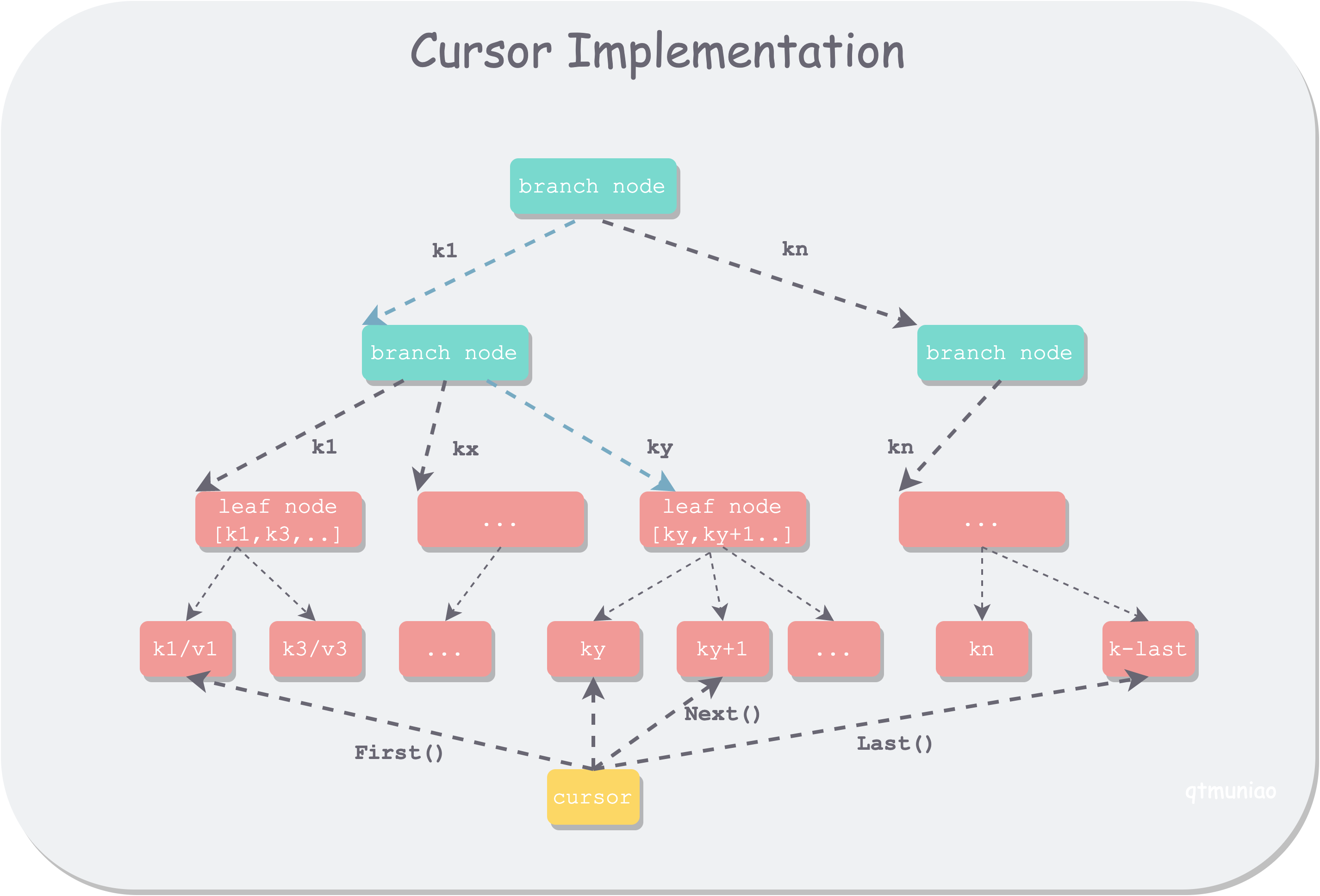
cursor 和某个 bucket 绑定,实现了以下功能,需要注意,当遍历到的元素为嵌套 bucket 时,value = nil。
1 | type Cursor |
由于 boltdb 中 B+ 树左右叶子节点并没有通过链表串起来,因此遍历时需要记下遍历路径以进行回溯。其结构体如下:
1 | type Cursor struct { |
elemRef 结构体如下,page 和 node 是一一对应的,如果 page 加载到了内存中(通过 page 转换而来),则优先使用 node,否则使用 page;index 表示路径经过该节点时在 inodes 中的位置。
1 | type elemRef struct { |
辅助函数
这几个 API 在实现的时候是有一些通用逻辑可以进行复用的,因此可以作为构件拆解出来。其中移动 cursor 在实现上,就是调整 cursor.stack 数组所表示的路径。
1 | // 尾递归,查询 key 所在的 node,并且在 cursor 中记下路径 |
组合遍历
有了以上几个基本构件,我们来梳一下主要 API 函数的实现:
1 | // 1. 将根节点放入 stack 中 |
这些 API 的实现叙述起来稍显繁琐,但只要抓住其主要思想,并且把握一些边界和细节,便能很容易看懂。主要思想比较简单: cursor 最终目的是在所有叶子节点的元素进行遍历,但是叶子节点并没有通过链表串起来,因此需要借助一个 stack 数组记下遍历上下文——路径,来实现对前驱后继的快速(因为前驱后继与当前叶子节点大概率共享前缀路径)访问。
另外需要注意的一些边界和细节如下:
- 每次移动,需要先找节点,再找节点中元素。
- 如果节点已经转换为 node,则优先访问 node;否则,访问 mmap 出来的 page。
- 分支节点所记元素的 key 为其指向的节点的 key,也即其节点所包含元素的最小 key。
- 使用 Golang 的
sort.Search获取第一个小于给定 key 的元素下标需要做一些额外处理。 - 几个边界判断,node 中是否有元素、index 是否大于元素值、该元素是否为子 bucket。
- 如果 key 不存在时,seek/search 定位到的是 key 应当插入的点。
树的生长
我们分几个时间节点来展开说明下 boltdb 中 B+ 树的生命周期:
- 数据库初始化时
- 事务开启后
- 事务提交时
最后在理解这几个阶段的状态的基础上,整个串一下其生长过程。
初始化时
数据库初始化时,B+ 树只包含一个空的叶子节点,该叶子节点即为 root bucket 的 root node。
1 | func (db *DB) init() error { |
之后 B+ 树的生长都由写事务中对 B+ 树节点的增删、调整来完成。按 boltdb 的设计,写事务只能串行进行。boltdb 使用 COW 的方式对节点进行修改,以保证不影响并发的读事务。即,将要修改的 page 读到内存,修改并调整后,申请新的 page 将变动后的 node 落盘。
这种方式可以方便的实现读写并发和事务,在本系列文章下一篇中将详细分析其原因。但无疑,其代价比较高昂,即使一个 key 的修改/删除,都会引起对应叶子节点所在 B+ 树路径上所有节点的修改和落盘。因此如果修改较频繁,最好在单个事务中做 Batch。
Bucket 较小时
在 bucket 包含的数据还很少时,不会给 bucket 开辟新的 page,而是将其内嵌(inline)在父 bucket 的叶子节点中。是否能内嵌的判断逻辑在 bucket.inlineable 中:
- 只包含一个叶子节点
- 数据尺寸不大于 1/4 个页
- 不包含子 bucket
事务开启后
在每次事务初始化时,会在内存中拷贝一份 root bucket 的句柄,以此作为之后动态加载修改路径上 node 的入口。
1 | func (tx *Tx) init(db *DB) { |
在读写事务中,用户调用 bucket.Put 新增或者修改数据时,涉及两个阶段:
- 查找定位:利用 cursor 定位到指定 key 所在 page
- 加载插入:加载路径上所有节点,并在叶子节点插入 kv
1 | func (b *Bucket) Put(key []byte, value []byte) error { |
查找定位。该实现逻辑在上一节所探讨的 cursor 的 cursor.seek 中,其主要逻辑为从根节点出发,不断二分查找,访问对应 node/page,直到定位到待插入 kv 的叶子节点。这里面有个关键的节点访问函数 bucket.pageNode,该函数不会加载 page 为 node,而只是复用已经缓存的 node ,或者直接访问 mmap 到内存空间中的相关 page。
加载插入。在该阶段,首先通过 cursor.node() 将 cursor 栈中保存的所有节点索引加载为 node,并缓存起来,避免重复加载以进行复用;然后通过 node.put 通过二分查找将 key value 数据插入叶子 node。
在只读事务中,只会有查找定位的过程,因此只会通过 mmap 对 page 访问,而不会有 page 到 node 的转换过程。
对于 bucket.Delete 操作,和上述两个阶段类似,只不过加载插入变成了加载删除。可以看出,这个阶段所有的修改都发生在内存中,文件系统中保存的之前 page 组成的 B+ 树结构并未遭到破坏,因此读事务可以并发进行。
事务提交前
在写事务开启后,用户可能会进行一系列的新增/删除,大量的相关节点被转化为 node 加载到内存中,改动后的 B+ 树由文件系统中的 page 和内存中的 node 共同构成,且由于数据变动,可能会造成某些节点元素数量过少、而另外一些节点元素数量过多。
因此在事务提交前,会先按一定策略调整 B+ 树,使其维持较好的查询性质,然后将所有改动的 node 序列化为 page 增量的写入文件系统中,构成一棵新的、持久化的、平衡的 B+ 树。
这个阶段涉及到两个核心逻辑:bucket.rebalance 和 bucket.spill, 他们分别对应节点的 merge 和 split,是维持 boltdb B+ 树查找性质的关键函数,下面来分别梳理下。
rebalance。该函数旨在将过小(key数太少或者总体尺寸太小)的节点合并到邻居节点上。调整的主要逻辑在 node.rebalance 中, bucket.rebalance 主要是个外包装:
1 | func (b *Bucket) rebalance() { |
node.rebalance 主要逻辑如下:
- 判断
n.unbalanced标记,避免对某个节点进行重复调整。使用标记的原因有二,一是按需调整,二是避免重复调整。 - 判断该节点是需要 merge,判断标准为:
n.size() > pageSize / 4 && len(n.inodes) > n.minKeys(),不需要则结束。 - 如果该节点是根节点,且只有一个孩子节点,则将其和其唯一的孩子合并。
- 如果该节点没有孩子节点,则删除该节点。
- 否则,将该节点合并到左邻。如果该节点是第一个节点,没左邻,则将右邻合并过来。
- 由于此次调整可能会导致节点的删除,因此向上递归看是否需要进一步调整。
需要明确的是,只有 node.del() 的调用才会导致 n.unbalanced 被标记。只有两个地方会调用 node.del():
- 用户调用
bucket.Delete函数删除数据。 - 子节点调用
node.rebalance进行调整时,删除被合并的节点。
而 2 又是由 1 引起的,因此可以说,只有用户在某次写事务中删除数据时,才会引起 node.rebanlance 主逻辑的实际执行。
spill,该函数功能有二,将过大(尺寸大于一个 page)节点拆分、将节点写入脏页(dirty page)。与 rebalance 一样,主要逻辑在 node.spill 中。不同的是,bucket.spill 中也有相当一部分逻辑,主要是处理 inline bucket 的问题。前面提到,如果一个 bucket 内容过少,就会直接内嵌在父 bucket 的叶子节点中。否则,则先调用子 bucket 的 spill 函数,然后将子 bucket 的根节点 pageid 放在父 bucket 叶子节点中。可以看出, spill 调整是一个自下而上的过程,类似于树的后序遍历。
1 | // spill 将尺寸大于一个节点的 page 拆分,并将调整后的节点写入脏页 |
node.spill 的主要逻辑如下:
- 判断
n.spilled标记,默认为 false,表明所有节点都需要调整。如果调整过,则跳过。 - 由于是自下而上调整,因此需要递归调用以先调整子节点,再调节本节点。
- 调整本节点时,将节点按照 pagesize 进行拆分。
- 为所有新节点申请新的合适尺寸的 pages,然后将 node 写入 page(此时还没有写回文件系统)。
- 如果 spilt 生成了新的根节点,则需要向上递归调用调整其他分支。为了避免重复调整,会将本节点
children置空。
可以看出,boltdb 维持 B+ 树查找性质,并非像教科书 B+ 树一样,将所有分支节点的分支树维护在一个固定范围,而是直接按节点元素是否能够保存到一个 page 中来做的。这样做可以减少 page 内部碎片,实现也相对简单。
这两个函数都通过 put/delete 后标记来实现按需调整,但不同的是,rebalance 先 merge 本身,再 merge 子 bucket;而 spill 先 split 子 bucket,再 split 本身。另外,调整时对他们调用顺序是有要求的,需要先调用 balance 进行无脑 merge,然后在调用 spill,按 pagesize 进行拆分后,写入脏页。
总结一下, 在 db 初始化时,只有一个页保存 root bucket 的根节点。之后的 B+ 树在 bucket.Create 的时候进行创建。初始时内嵌在父 bucket 的叶子节点中,读事务不会对 B+ 树结构造成任何改变,写事务中所有变动,会先写到内存中,在事务提交时,会进行平衡调整,然后增量的写入文件系统。随着写入数据的增多,B+ 树会不断进行拆分,变深,不在内嵌于父 bucket 中。
小结
boltdb 使用类 B+ 树组织数据库索引,所有数据存在叶子节点,分支节点只用于路由查找。boltdb 支持 bucket 间的嵌套,在实现上表现为 B+ 树的嵌套,通过 page id 来维持父子 bucket 间的引用。
boltdb 中的 B+ 树为了实现简单,没有使用链表将所有叶子节点串在一起。为了支持对数据的顺序遍历,额外实现了一个 curosr 遍历逻辑,通过保存遍历栈来提高遍历效率、快速跳转。
boltdb 对 B+ 树的生长以事务为周期,而且生长只发生在写事务中。在写事务开始后,会复制 root bucket 的根节点,然后将改动涉及到的节点按需加载到内存,并在内存中进行修改。在写事务结束前,在对 B+ 树调整后,将所有改动涉及到的 node 申请新的 page,写回文件系统,完成 B+ 树一次生长。释放的树节点,在没有读事务占用后,会进入 freelist 供之后使用。
注解
节点:B+ 树中的节点,在文件系统或者 mmap 后表现为 page,在内存中转换后成为 node。
路径:树中的路径指树的根节点到当前节点的顺序经过的所有节点。
参考
- boltdb repo:https://github.com/boltdb/bolt

