由于对各种矩阵运算物理意义的理解总是跟不上,因此尽管多年多次尝试入门机器学习,却总是被拒之门外。偶然间同事推荐了 MIT 那门经典的线性代数公开课,听了几节,煞是过瘾,之前紧闭的大门竟有打开一丝的感觉。
因此,本系列会在每篇文章分享一些课程中有意思的点。为了避免晦涩,每章会尽可能去上下文、保持简短,请放心食用。也因此,本系列会牺牲一些精确性,且并无体系化,仅仅旨在唤起你一丢丢兴趣。注:例子都由 KimiChat 生成。
作者:木鸟杂记 https://www.qtmuniao.com/2024/06/29/interesting-linear-algebra-1/ 转载请注明出处
右乘列向量
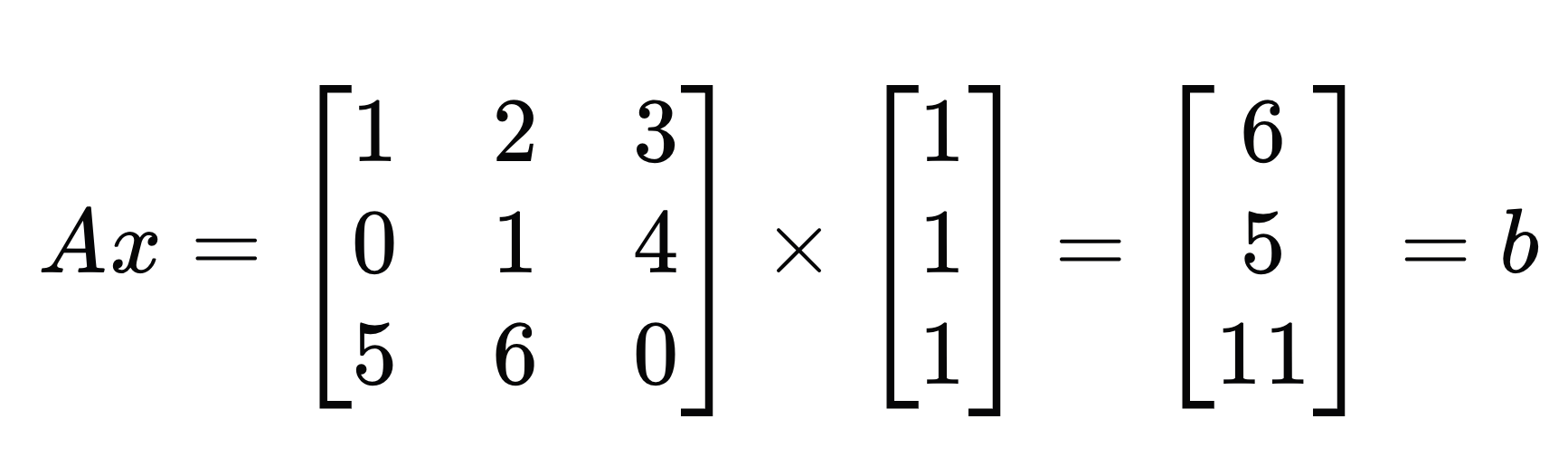
对于一个方阵 A 来说,右乘一个列向量 x,可以理解为:使用 x 中的值作为权重,对 A 中列向量进行线性组合,得到一个新的列向量 b。
利用该理解对上图拆开一下就是:
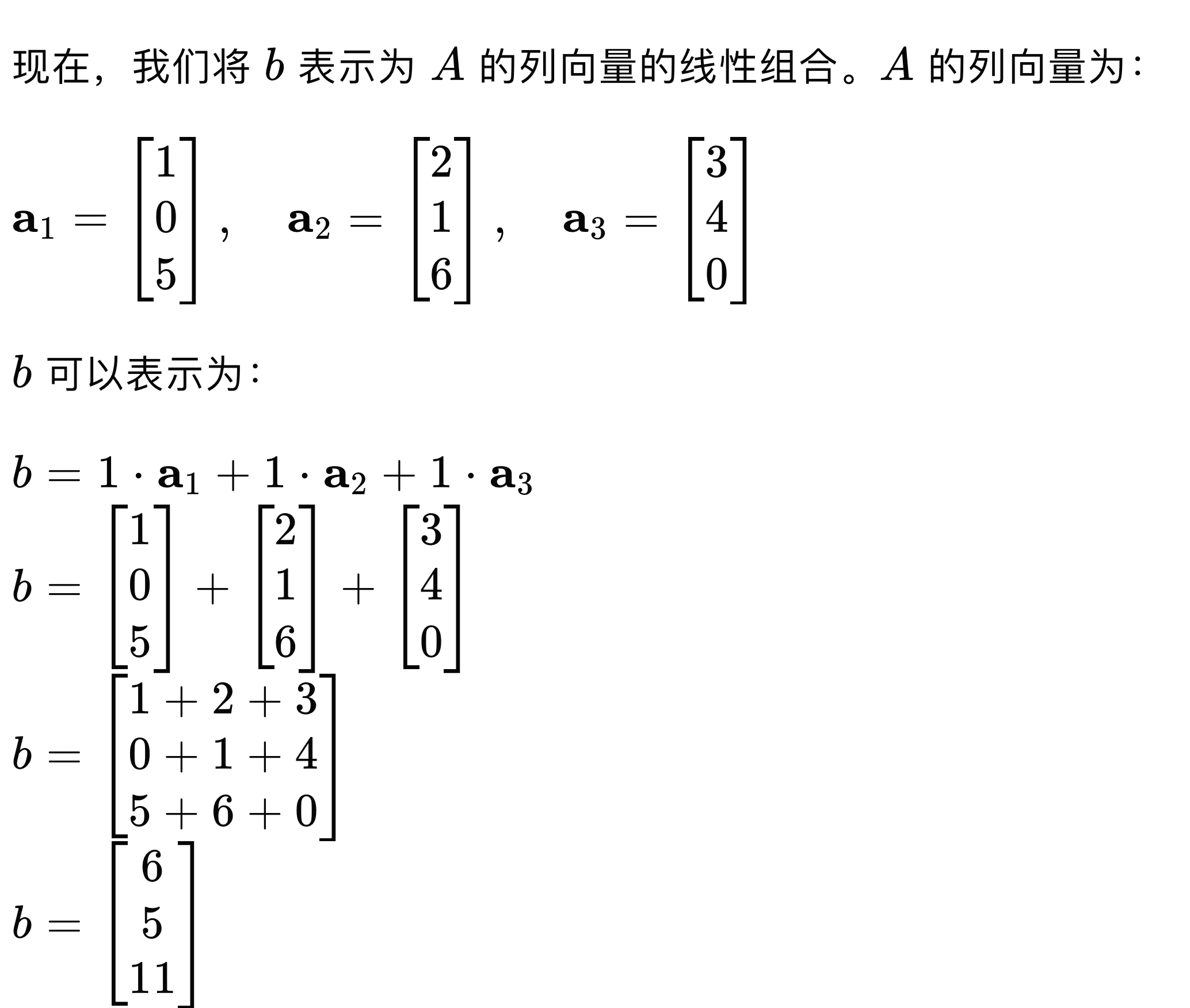
注:这其中会要求一些性质,比如 A 是可逆矩阵(invertible matrix),或者是非奇异(non singular matrix),但这些名词我们就不在此深究了,感兴趣的可以去看视频。
左乘行向量
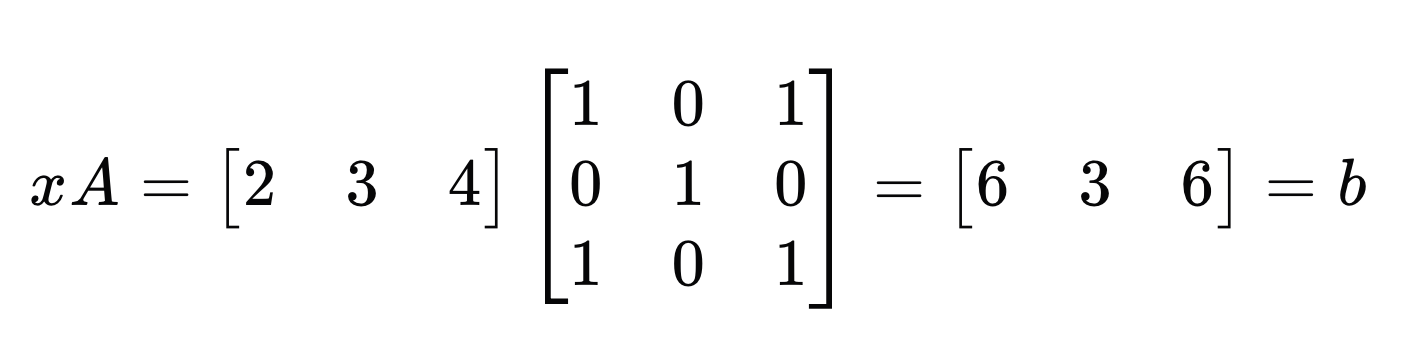
对于一个方阵 A 来说,左乘一个行向量 x,可以理解为:使用 x 中的值作为权重,对 A 中行向量进行线性组合,得到一个新的行向量 b。
拆解下过程,就是:
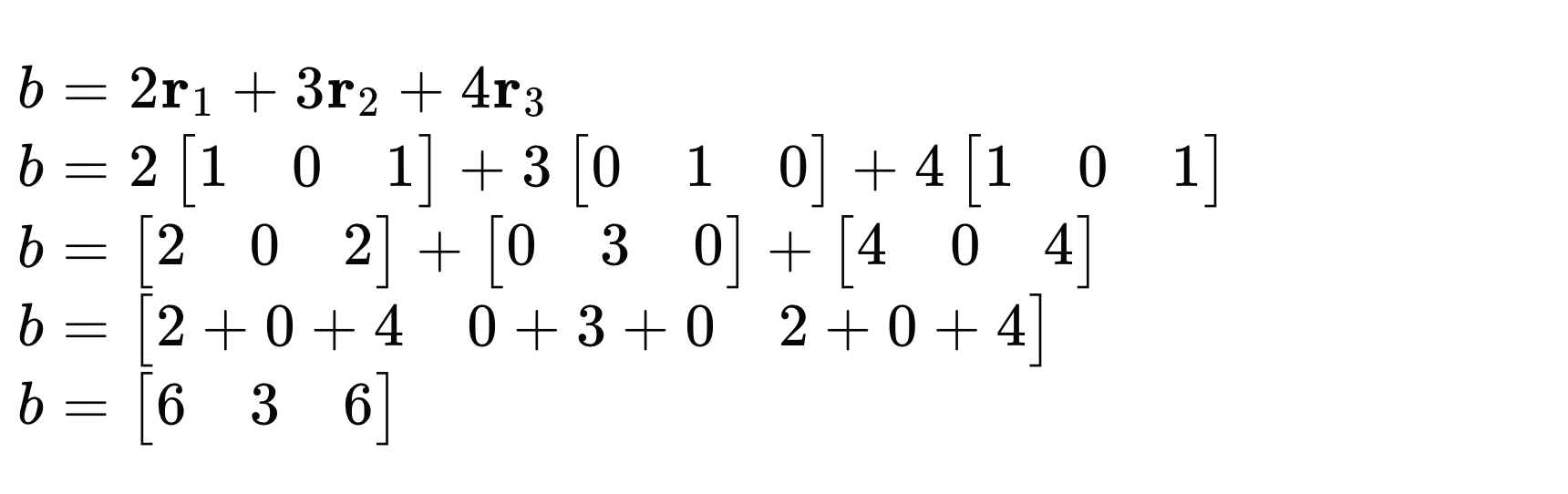
扩展
有了上述直觉,我们就可以扩展一下,拆解矩阵乘法了。
比如利用右乘行向量拆解。
A * X = B
可以拆解为:
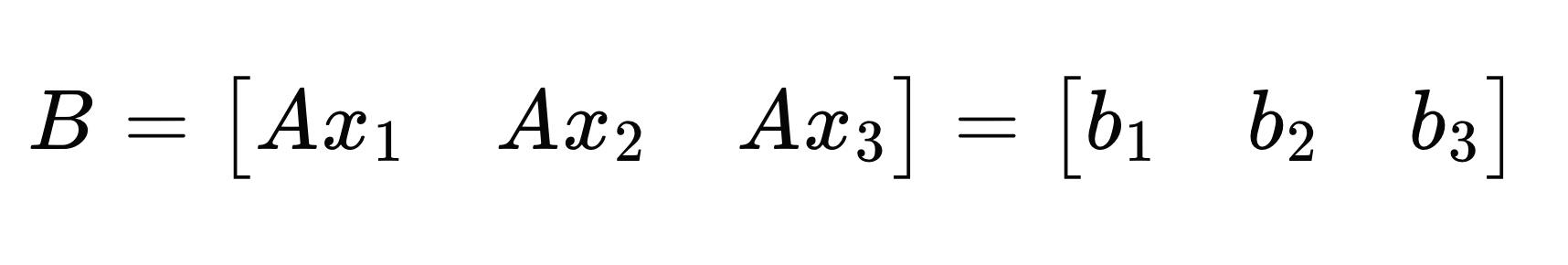
即,利用 X 中三列分别对 A 进行线性组合,得到结果 B 中的三列。
同样,也可以利用左乘行向量对上述乘法进行拆解,可以自己试试。
小结
当然,有时候,这种思想有时候可能会使得简单的运算变复杂。但学多了就会发现,对于线代中同一个公式会有多种“物理理解”,每种理解方法都会有其特定适用场景,多在工具箱里积累一些工具方法,会使得我们对矩阵运算这种高维思维更加得心应手。

